User-defined preconditioning of local solver in HybridisationPC

[sv2518]

This PR is based on my other two PRs. The only commit of relevance is the last one, 85a02cf.

In this PR I introduce a PETSc option which allows users to provide an approximation to the Schur complement in the reconstruction calls which is then used as a preconditioner to the local system solve.

If we are doing hybridised mixed Poisson e.g., we know that this is a good idea (and already advise our users to try in this demo https://www.firedrakeproject.org/demos/saddle_point_systems.py.html). The argument to provide an approximation to the Schur complement is that the Schur complement's condition number is increasing with increasing amount of cells. By providing an approximation to the Schur complement and using it as a preconditioner we essentially lower the condition number.

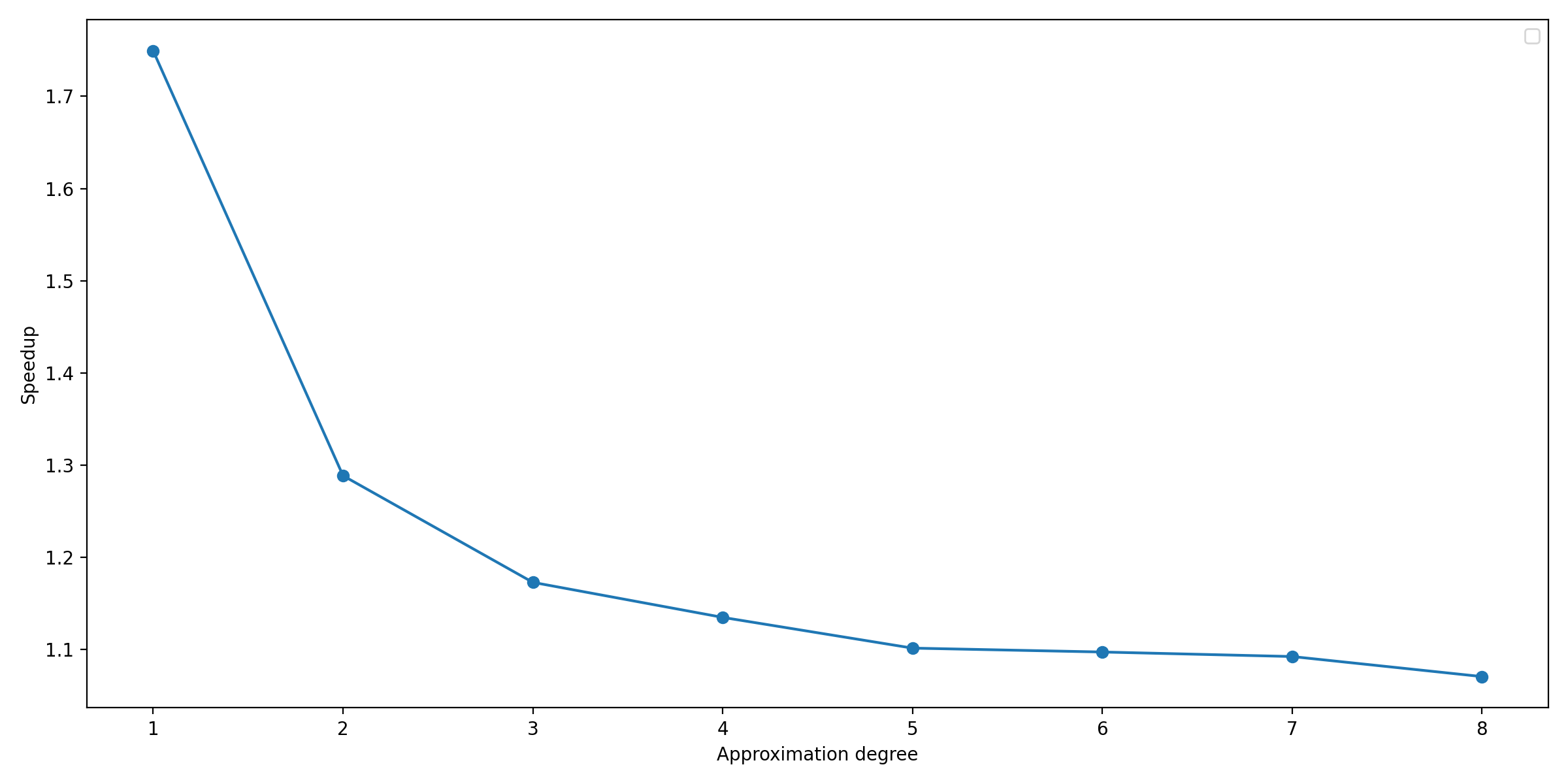
The difference to the demo is that we are doing the solve on a local level (on a unit cell, h=1), but the condition number does not only depend on the mesh size parameter h, but also on the approximation degree p.

I have provided a test for a mixed Poisson problem and looked at the condition numbers of the local operators. Without preconditioning the Schur complement S has condition number 16.77 for the given discretisation, and 5.95 for the preconditioned Schur complement P*S. The condition numbers would be higher if I had chosen a high approximation degree.

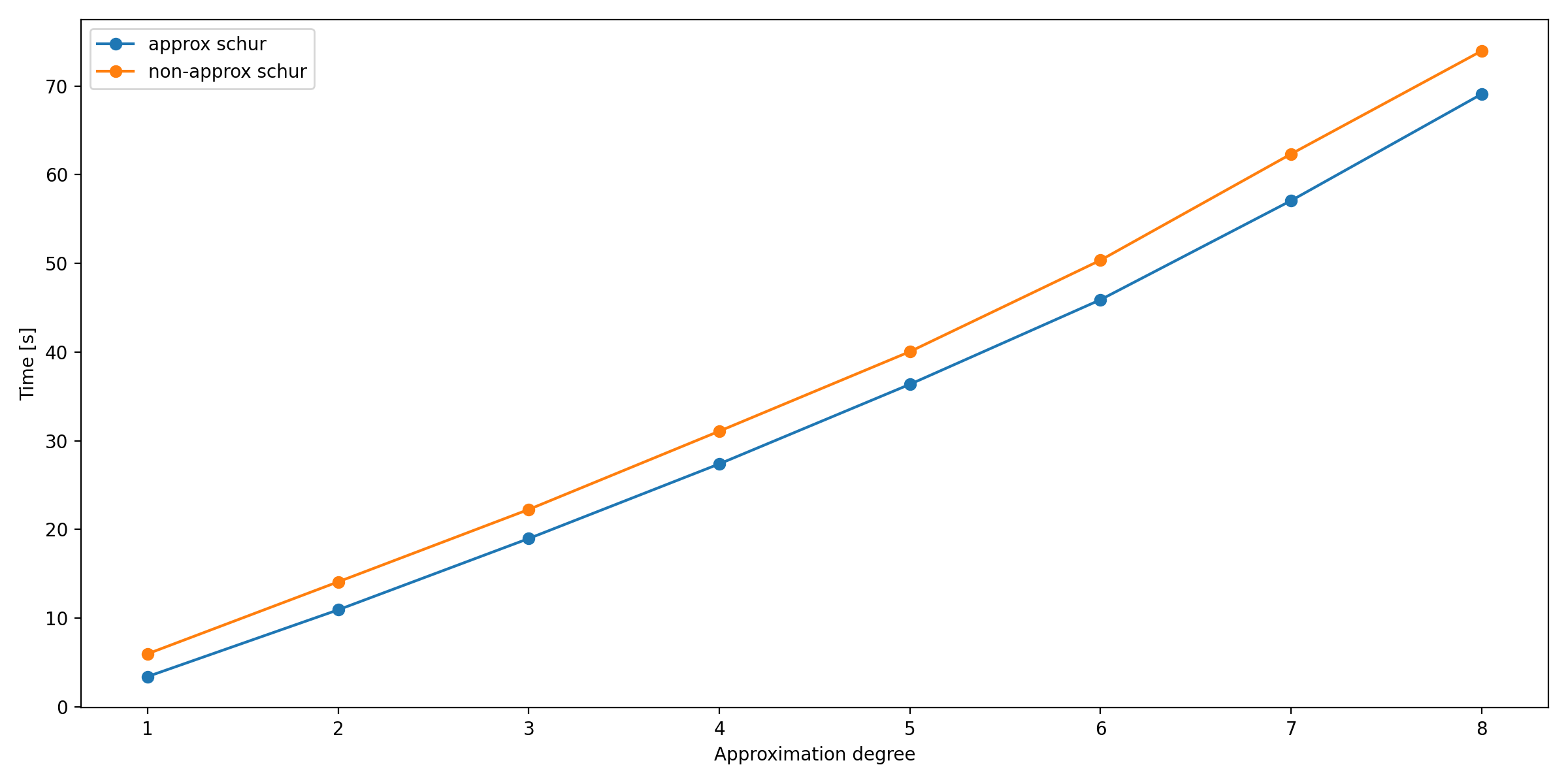
So from looking at the condition numbers I would say yes, this a good idea but I am not sure if we already profit from this with the code infrastructure that we have on master at the moment. The way I build the system is by simply solving P^{-1} * S x = P^{-1} b locally and we can't do local actions yet, so all the operators here are all dealt with in a matrix-explicit manner. With the preconditioner we need to build more matrices, and the trade-off might not pay off.

So I did some timings and as expected I think I have the same issue as in my other PR. It does pay off to do this but the speedup is limited at higher order due a dominating cost of data transfer.

[dham]

Subject to upstream changes landing.

[sv2518]

OK, I cleaned this up and rebased on top of master. When the other PR is merged I will still need to drop the first commit.

[sv2518]

Hey, I converted this to draft now actually. I am currently working on preparing another PR that is similar to this one, but introduces diagonal local preconditioners. Since this started to be quite invasive in the hybridisation PR I refactored recent changes of the hybridisation PR into a separate class (including the changes in this PR), so maybe we want to hold of on this one until I finished the diagonal PR.

[sv2518]

This will be swallowed by #2259, so I close.